
 |
|
|
Главная --> Справочник терминов Реологических уравнениях а - действие внешних сил (напряжений) [ / - всестороннее сжатие; 2 - сдвиг; 3 - растяжение (удлинение)]; б - виды деформации [1 - всестороннее сжатие; 2 а 2' - сдвиг (простой и чистый соответственно); 3 - растяжение]; в - графическое изображение реологических уравнений состояния [1 - идеально упругое тело (закон Гука); 2 - идеальная жидкость (закон Ньютона); 3 - пластическое тело] В соответствии с двумя видами систем координат существуют и два класса реологических уравнений: содеформированные и совращающиеся. Любое уравнение, записанное в одной системе координат, можно трансформировать в другую, а также в неподвижную (лабораторную) систему координат, в которой получают экспериментальные результаты и записывают уравнения баланса. Эти преобразования более громоздки, чем преобразования из субстанциональной координатной системы в неподвижную (см. разд. 5.1) **, хотя и аналогичны им. В последующих трех разделах будут обсуждены три из упомянутых реологических уравнений: ЛВУ, ОНЖ и КЭФ. Первое вскрывает вязкоупругую природу поведения расплавов полимеров; различные частные виды второго широко применяются для решения задач по переработке полимеров; с помощью третьего уравнения можно предсказывать разности нормальных напряжений в установившихся сдвиговых течениях, что полезно в вискозиметрии. Существует большое число других частных реологических уравнений, описывающих вязкое или вязкоупругое, а также и более сложное поведение различных реальных материалов. Из них особый интерес представляют уравнения, учитывающие тиксотропные свойства каучуков и особенно резиновых смесей. Их кажущийся предел текучести и пластичность играют большую роль в процессах переработки (смешение, вальцевание, каландрование), а также при хранении заготовок на технологических складах (когда важна их «каркасность»). Дальнейшие попытки улучшить соответствие теории с экспериментом привели к появлению ряда других реологических уравнений, носящих в значительной мере эмпирический характер. Среди них наиболее широкое распространение нашло уравнение Муни—Ривлина! Дальнейшие попытки улучшить соответствие теории с экспериментом привели к появлению ряда других реологических уравнений, носящих в значительной мере эмпирический характер. Среди них наиболее широкое распространение нашло уравнение Муни—Ривлина! Известно много подходов к выводу реологических уравнений состояния, удовлетворяющих сформулированным выше условиям10^21. Все они по существу сводятся к построению систем преобразования реологического уравнения состояния, заданного в конвективной системе координат, вмороженной в движущийся и деформирующийся элемент среды, к неподвижной физической системе координат, в которой рассматриваются уравнения неразрывности и закон сохранения момента количества движения. Известно много подходов к выводу реологических уравнений состояния, удовлетворяющих сформулированным выше условиям. Все они, по существу, сводятся к построению систем преобразования реологического уравнения состояния, заданного в конвективной системе координат, вмороженной в движущийся и деформирующийся элемент среды, к неподвижной физической системе координат, в которой рассматриваются уравнения неразрывности и закон сохранения момента количества движения [32, 33, 158—163]. деформация соизмерима по величине с пластической деформацией. В установившихся режимах, когда изменение высокоэластической деформации отсутствует, доминируют вязкостные эффекты, которые удовлетворительно описываются более простыми формами реологических уравнений. 3.7. Тензоры деформаций по Коши — Грину и Фингеру. Рассмотрение простого сдвига позволяет ввести понятия о еще двух тензорах, характеризующих деформацию в окрестности данной точки. Они часто используются в литературе применительно к условиям сдвига, а также для записи полных реологических уравнений состояния (см. ниже). Для этого вернемся к анализу формулы (1.13) и представим ее в следующем виде: Она обычно применяется при построении реологических уравнений состояния вязкой жидкости (см. ниже). Функции F и W* имеют различный вид для разных групп материалов; отдельные материалы в каждой группе различаются значениями параметров в реологических уравнениях. Локальный векторный базис, «вмороженный» в деформируемый материал, позволяет наиболее естественным образом описывать различные реологические состояния, поскольку при этом любые вращения материального элемента как целого и квазитвердые переносы не будут отражаться на соответствующих реологических уравнениях, описывающих в данном случае только девиаторные и изотропные деформации (формоизменения). Функции Ф и D имеют различный вид для разных групп материалов и отдельные материалы в каждой группе различаются параметрами в их реологических уравнениях. В частности, этими параметрами могут быть механические материальные константы. 5. О реологических уравнениях состояния.. 49 5. О реологических уравнениях состояния анализе кинематики движущейся среды, когда была показана необходимость перехода от конвективной к пространственной системе координат. Этот принцип означает, что при установлении связей между различными величинами они должны относиться к одной и той же точке пространства или среды. Поэтому если в реологических уравнениях состояния встречаются производные любых величин по времени, то их следует вычислять с учетом смещений среды в пространстве, т. е. учитывать движение среды как целого и вращение элементов среды в окрестности рассматриваемых точек. Формально это требует использования в реологических уравнениях состояния не частных производных величин по времени, а производных, при вычислении которых учитывались бы рассмотренные выше преобразования координат точек (относительно фиксированной координатной системы) во времени. Примерами таких производных являются операторы по Олдройду и по Яуманну. Заметим, что аналогичные по смыслу преобразования должны быть проделаны не только в отношении производных по времени, но и в отношении интегралов, которые суммируют совокупность эффектов, имевших место на предшествующих стадиях деформирования по отношению к данному текущему моменту времени. Поэтому при записи реологических уравнений состояния с использованием таких интегралов должны учитываться правила перехода от конвективной системы координат к пространственной, когда при движении во все предыдущие моменты времени (по отношению к данному текущему моменту) изменялись положения точек тела'и связанных с ними координат. Отвечающие этим представлениям математические операции будут рассмотрены ниже, там, где будут использоваться соответствующие интегралы для определения реологических уравнений состояния. Последний вопрос, на котором следует остановиться в этом разделе, относится к тому, как в реологических уравнениях состояния учитываются различия в физической природе разнообразных сред. Согласно всему сказанному выше это делается двояко. В первую очередь, свойства различных сред могут описываться различными 9.2. Реологические уравнения состояния систем со спектром, •зависящим от режима деформирования. Использование различных мер деформации в интегральных реологических уравнениях состояния (1.109) может рассматриваться как следствие влияния внешнего воздействия на систему, приводящего в результате к изменению •ее релаксационных свойств. Действительно, формулу (1.109) можно представить следующим образом: Распределение времен релаксации может быть непрерывным, как в рассматривавшихся выше интегральных реологических уравнениях состояния, и дискретным, подобно моделям, построенным из параллельно соединенных максвелловских элементов. Ради простоты рассмотрим течение в режиме простого сдвига для системы с непрерывным распределением частот релаксации. В некоторой дифференциально малой части спектра, релаксационная частота которого заключена в пределах от s до (s + ds), эффективный модуль, характеризующий эту часть спектра N (s) ds, а вязкость N (s)/s ds. Упругая энергия Е (s)ds, накапливаемая в процессе сдвигового течения структурными элементами, ответственными за релаксацию с частотой от s до (s + ds), равна В заключение рассмотрения вопроса о реологических уравнениях состояния, получаемых на основе теорий нелинейной вязкоупру-гости, следует указать на важность того, чтобы в них входило минимальное число констант; это существенно облегчает их экспериментальное определение и, следовательно, практическое использование. Важнейшим способом определения констант в уравнениях состояния является анализ гармонических режимов нагружения с малыми амплитудами. Тогда все обобщения операторного уравнения (1.100) вырождаются в уравнение (1.100) с частными производными a if и у ^ по времени. Определение констант ап и Ьп, а через них набора времен релаксации становится простой задачей гармонического анализа данных, полученных при измерении динамических свойств материала. Многие важные случаи такого анализа будут рассмотрены в главе, посвященной описанию динамических свойств полимерных систем. 3.1. Нормальные напряжения в различных реологических уравнениях состояния. При одномерном сдвиговом течении ньютоновской жидкости нормальных напряжений, отличных от гидростатического давления, не существует. Это непосредственно следует из реологического уравнения состояния ньютоновской жидкости, поскольку напряжения, возникающие при ее течении, сг//, зависят только от компонент тензора скоростей деформации с теми же индексами. Поэтому, если ylt = О, то и а ц = 0. В вязких жидкостях, реологические свойства которых описываются более сложными уравнениями состояния, чем ньютоновской жидкости, возможно появление нор-нальных напряжений при сдвиговом течении. 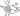 Ректификационной установки Рекуперативного теплообменника Релаксацией напряжения Релаксации процессов Релаксации уменьшается Релаксационных процессах Релаксационным переходам Распыленном состоянии Релаксацию напряжений |
- |